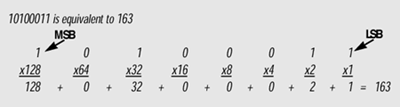
[an error occurred while processing this directive]
It wasn't until the Twentieth Century, however, that binary mathematics was applied to the recording, transmission, or manipulation of sounds or pictures. The problem was largely technological. First, there wasn't even electronic sound (let alone pictures) to record, transmit, or manipulate until the end of the Nineteenth Century. Second, the circuitry required to digitize even a simple telephone call didn't exist until shortly before that feat was achieved in 1939 (analog-to-digital converters slowed things down; digitally generated speech and music predated the digitization of sound, just as computer graphics predated the digital video timebase corrector and international standards converter).
Scientists working on digital signals weren't even able to use today's common term for the little pieces of information they dealt with until 1948. In July of that year, in the Bell System Technical Journal, Claude Shannon, considered by many the creator of information theory, credited J. W. Tukey with suggesting a contraction of the words binary digit into bit. But the word digital definitely comes from the Latin digitus, which means fingers and toes, making the first digital effects finger shadow puppets on a wall, and the first digital compression a squeezed finger or toe.
--Mark Schubin
In order to understand digital, you must first understand that everything in nature, including the sounds and images you wish to record or transmit, was originally analog. The second thing you must understand is that analog works very well. In fact, because of what analog and digital are, a first-generation analog recording can be a better representation of the original images than a first-generation digital recording. This is because digital is a coded approximation of analog. With enough bandwidth, a first-generation analog VTR can record the more "perfect" copy.
Digital is a binary language represented by zeros (an "off" state) and ones (an "on" state). Because of this, the signal either exists (on) or does not exist (off). Even with low signal power, if the transmitted digital signal is higher that the background noise level, a perfect picture and sound can be obtained--on is on no matter what the signal strength.
The Language Of Digital: Bits & Bytes
Bit is short for Binary digit and is the smallest data unit in a digital system. A bit is a single one or zero. Typically 8-bits make up a byte (although byte "words" can be 10-bit, 16-bit, 24-bit, or 32-bit).
In an 8-bit system there are 256 discrete values. The mathematics is simple: It is the number two (as in binary) raised to the power of the number of bits. In this case 28=256. A 10-bit system has 1,024 discrete values (210=1,024). Notice that each additional bit is a doubling of the number of discrete values.
Here's how this works, as each bit in the 8-bit word represents a distinct value:
The more bits, the more distinct the value. For example, a gray-scale can be represented by 1-bit which would give the scale two values (21=2): 0 or 1 (a gray-scale consisting of white and black). Increase the number of bits to two-bits and the gray-scale has four values (22=4): 0, 1, 2, and 3, where 0=0 percent white (black), 1=33 percent white, 2=67 percent white, and 3=100 percent white. As we increase the number of bits, we get more accurate with our gray-scale.
In digital video, black is not at value 0 and white is neither at value 255 for 8-bit nor 1,023 for 10-bit. To add some buffer space and to allow for "superblack" (which is at 0 IRE while regular black is at 7.5 IRE), black is at value 16 while white is at value 235 for 8-bit video. For 10-bit video, we basically multiply the 8-bit numbers by four, yielding black at a value of 64 and white at a value of 940.
Also keep in mind that while digital is an approximation of the analog world--the actual analog value is assigned to its closest digital value--human perception has a hard time recognizing the fact that it is being cheated. While very few expert observers might be able to tell that something didn't look right in 8-bit video, 10-bit video looks perfect to the human eye. But as you'll see in Chapter 4: Audio, human ears are not as forgiving as human eyes--in audio most of us require at least 16-bit resolution--while experts argue that 20-bit, or ultimately even 24-bit technology needs to become standard before we have recordings that match the sensitivity of human hearing.
Digitizing: Analog To Digital
To transform a signal from analog to digital, the analog signal must go through the processes of sampling and quantization. The better the sampling and quantization, the better the digital image will represent the analog image.
Sampling is how often a device (like an analog-to-digital converter) samples a signal. This is usually given in a figure like 48 kHz for audio and 13.5 MHz for video. It is usually at least twice the highest analog signal frequency (known as the Nyquist criteria). The official sampling standard for standard definition television is ITU-R 601 (short for ITU-R BT.601-2, also known as "601").
For television pictures, eight or 10-bits are normally used; for sound, 16 or 20-bits are common, and 24-bits are being introduced. The ITU-R 601 standard defines the sampling of video components based on 13.5 MHz, and AES/EBU defines sampling of 44.1 and 48 kHz for audio.
Quantization can occur either before or after the signal has been sampled, but usually after. It is how many levels (bits per sample) the analog signal will have to force itself into. As noted earlier, a 10-bit signal has more levels (resolution) than an 8-bit signal.
Errors occur because quantizing a signal results in a digital approximation of that signal.
When Things Go Wrong: The LSB & MSB
Things always go wrong. Just how wrong is determined by when that "wrongness" occurred and the length of time of that "wrongness."
Let's take an 8-bit byte as an example:
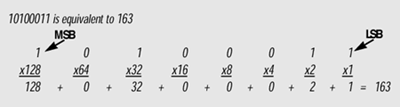
The "1" on the far right that represents the value 1 is called the least significant bit (LSB). If there is an error that changes this bit from "1" (on) to "0" (off), the value of the byte changes from 163 to 162--a very minor difference. But the error increases as problems occur with bits more towards the left.
The "1" on the left that represents the value 128 is called the most significant bit (MSB). An error that changes this bit from "1" (on) to "0" (off) changes the value of the byte from 163 to 35--a very major difference. If this represented our gray-scale, our sample has changed from 64 percent white to only 14 percent white.
An error can last short enough to not even affect one bit, or long enough to affect a number of bits, entire bytes, or even seconds of video and audio.
If our error from above lasted in duration the amount of time to transmit two bits, the error can be anywhere from minor (if it is the LSB and the bit to its left) to major (if it is the MSB and the bit to its right).
Where and how long errors occur is anyone's guess, but as you'll see below in Error Management, digital gives us a way to handle large errors invisibly to the viewer.
By Glen Pensinger
Ratios such as 4:2:2 and 4:1:1 are an accepted part of the jargon of digital video, a shorthand taken for granted and sometimes not adequately explained.
With single-channel, composite signals such as NTSC and PAL, digital sampling rates are synchronized at either two, three, or four times the subcarrier frequency. The shorthand for these rates is 2fsc, 3fsc, and 4fsc, respectively.
With three-channel, component signals, the sampling shorthand becomes a ratio. The first number usually refers to the sampling rate used for the luminance signal, while the second and third numbers refer to the rates for the red and blue color-difference signals.
A 14:7:7 system would be one in which a wideband luminance signal is sampled at 14 MHz and the narrower bandwidth color-difference signals are each sampled at 7 MHz.
As work on component digital systems evolved, the shorthand changed. At first, 4:2:2 referred to sampling luminance at 4fsc (about 14.3 MHz for NTSC) and color-difference at half that rate, or 2fsc.
Sampling schemes based on multiples of NTSC or PAL subcarrier frequency were soon abandoned in favor of a single sampling standard for both 525- and 625-line component systems. Nevertheless, the 4:2:2 shorthand remained.
In current usage, "4" usually represents the internationally agreed upon sampling frequency of 13.5 MHz. Other numbers represent corresponding fractions of that frequency.
A 4:1:1 ratio describes a system with luminance sampled at 13.5 MHz and color-difference signals sampled at 3.375 MHz. A 4:4:4:4 ratio describes equal sampling rates for luminance and color difference channels as well as a fourth, alpha key signal channel. A 2:1:1 ratio describes a narrowband system that might be suitable for consumer use and so on.
The shorthand continues to evolve. Contrary to what you might expect from the discussion above, the 4:2:0 ratio frequently seen in discussions on MPEG compression does not indicate a system without a blue color-difference component. Here, the shorthand describes a video stream in which there are only two color difference samples (one red, one blue) for every four luminance samples.
Unlike 4:1:1, however, the samples in 525 line systems don't come from the same line as luminance, but are averaged from two adjacent lines in the field. The idea was to provide a more even and averaged distribution of the reduced color information over the picture.
(See Chapter 3: Pre-Production, for a comparison of resolutions for different videotape and disk formats.)
By Glen Pensinger
Some people say that compressing video is a little like making orange juice concentrate or freeze-dried back-packing food. You throw something away (like water) that you think you can replace later. In doing so, you gain significant advantages in storage and transportation and you accept the food-like result because it's priced right and good enough for the application. Unfortunately, while orange juice molecules are all the same, the pixels used in digital video might all be different.
Video compression is more like an ad that used to appear in the New York City subway which said something like: "If u cn rd ths, u cn get a gd pying jb" or personalized license plates that don't use vowels (nmbr-1). You understand what the message is without having to receive the entire message--your brain acts as a decoder. Email is taking on this characteristic with words such as l8r (later) and ltns (long time no see).
Why Compress?
There is a quip making the rounds that proclaims "compression has never been shown to improve video quality." It's popular with folks who think compression is a bad compromise. If storage costs are dropping and communication bandwidth is rapidly increasing, they reason, why would we want to bother with anything less than "real" video? Surely compression will fall by the wayside once we've reached digital perfection.
Other people, like Avid Technology VP Eric Peters, contend that compression is integral to the very nature of media. The word "media," he points out, comes from the fact that a technology, a medium, stands between the originator and the recipient of a message. Frequently that message is a representation of the real world. But no matter how much bandwidth we have, we will never be able to transmit all of the richness of reality. There is, he argues, much more detail in any source than can possibly be communicated. Unless the message is very simple, our representation of it will always be an imperfect reduction of the original. Even as we near the limits of our senses (as we may have with frequency response in digital sound) we still find there is a long way to go. People perceive many spatial and other subtle clues in the real world that are distorted or lost in even the best digital stereo recordings.
Furthermore, the notion of quality in any medium is inherently a moving target. We've added color and stereo sound to television. Just as we start to get a handle on compressing standard definition signals, high definition and widescreen loom on the horizon. There will never be enough bandwidth. There is even a Super High Definition format that is 2048x2048 pixels--14 times as large as NTSC.
Perhaps former Tektronix design engineer Bruce Penny countered the quip best when he said, "Compression does improve picture quality. It improves the picture you can achieve in the bandwidth you have."
Compression Basics
Compression comes in a number of flavors, each tailored for a specific application or set of applications. An understanding of the compression process will help you decide which compression method or group of methods are right for you.
Compression Ratio
The essence of all compression is throwing data away. The effectiveness of a compression scheme is indicated by its "compression ratio," which is determined by dividing the amount of data you started with by what's left when you're through.
Assuming a high definition camera spits out around one billion video bits a second, and this is ultimately reduced to something around 18 million bits for broadcast in the ATSC system, the compression ratio is roughly 55:1.
However, don't put too much stock in compression ratios alone. On a scale of meaningful measures, they rank down somewhere with promised savings on long distance phone calls. To interpret a compression ratio, you need to know what the starting point was.
For a compression system that puts out a 25 megabit per second (Mbps) video stream, the compression ratio would be about 8.5:1 if the starting point was 485x740 pixels, 4:2:2, 10-bit sampled, 30 frames per second (fps) pictures. If, however, the starting video was 480x640, 4:1:1, 8-bit, 30 fps, the ratio would be about 4.5:1.
Lossless Versus Lossy
There are two general types of compression algorithms: lossless and lossy. As the name suggests, a lossless algorithm gives back the original data bit-for-bit on decompression.
One common lossless technique is "run length encoding," in which long runs of the same data value are compressed by transmitting a prearranged code for "string of ones" or "string of zeros" followed by a number for the length of the string.
Another lossless scheme is similar to Morse Code, where the most frequently occurring letters have the shortest codes. Huffman or entropy coding computes the probability that certain data values will occur and then assigns short codes to those with the highest probability and longer codes to the ones that don't show up very often. Everyday examples of lossless compression can be found in the Macintosh Stuffit program and WinZip for Windows.
Lossless processes can be applied safely to your checkbook accounting program, but their compression ratios are usually low--on the order of 2:1. In practice these ratios are unpredictable and depend heavily on the type of data in the files.
Alas, pictures are not as predictable as text and bank records, and lossless techniques have only limited effectiveness with video. Work continues on lossless video compression. Increased processing power and new algorithms may eventually make it practical, but for now, virtually all video compression is lossy.
Lossy video compression systems use lossless techniques where they can, but the really big savings come from throwing things away. To do this, the image is processed or "transformed" into two groups of data. One group will, ideally, contain all the important information. The other gets all the unimportant information. Only the important stuff needs to be kept and transmitted.
Perceptual Coding
Lossy compression systems take the performance of our eyes into account as they decide what information to place in the important pile and which to discard in the unimportant pile. They throw away things the eye doesn't notice or won't be too upset about losing.
Since our perception of fine color details is limited, chroma resolution can be reduced by factors of two, four, eight or more, depending on the application.
Lossy schemes also exploit our lessened ability to see detail immediately after
a picture change, on the diagonal or in moving objects. Unfortunately, the latter doesn't yield as much of a savings as one might first think, because we often track moving objects on a screen with our eyes.
Predictive Coding
Video compression also relies heavily on the correlation between adjacent picture elements. If television pictures consisted entirely of randomly valued pixels (noise), compression wouldn't be possible (some music video producers and directors are going to find this out the hard way--as encoders lock-up). Fortunately, adjoining picture elements are a lot like the weather. Tomorrow's weather is very likely to be just like today's, and odds are that nearby pixels in the same or adjacent fields and frames are more likely to be the same than they are to be different.
Predictive coding relies on making an estimate of the value of the current pixel based on previous values for that location and other neighboring areas. The rules of the estimating game are stored in the decoder and, for any new pixel, the encoder need only send the difference or error value between what the rules would have predicted and the actual value of the new element. The more accurate the prediction, the less data needs to be sent.
Motion Compensation
The motion of objects or the camera from one frame to the next complicates predictive coding, but it also opens up new compression possibilities. Fortunately, moving objects in the real world are somewhat predictable. They tend to move with inertia and in a continuous fashion. In MPEG, where picture elements are processed in blocks, you can save quite a few bits if you can predict how a given block of pixels has moved from one frame to the next. By sending commands (motion vectors) that simply tell the decoder how to move a block of pixels already in its memory, you avoid resending all the data associated with that block.
Inter- Versus Intra-frame Compression
As long as compressed pictures are only going to be transmitted and viewed, compression encoders can assign lots of bits into the unimportant pile by exploiting the redundancy in successive frames. It's called "inter-frame" coding.
If, on the other hand, the video is destined to undergo further processing such as enlargement, rotation and/or chromakey, some of those otherwise unimportant details may suddenly become important, and it may be necessary to spend more bits to accommodate what post production equipment can "see."
To facilitate editing and other post processing, compression schemes intended for post usually confine their efforts within a single frame and are called "intra-frame." It takes more bits, but it's worth it.
The Ampex DCT videocassette format, Digital Betacam, D9 (formerly Digital-S), DVCPRO50, and various implementations of Motion-JPEG are examples of post
production gear using intra-frame compression. The MPEG 4:2:2 Profile can also be implemented in an intra-frame fashion.
SYMMETRICAL VERSUS ASYMMETRICAL
Compression systems are described as symmetrical if the complexity (and therefore cost) of their encoders and decoders are similar. This is usually the case with recording and professional point-to-point transmission systems. With point-to-multipoint transmission applications, such as broadcasting or mass program distribution where there are few encoders but millions of decoders, an asymmetrical design may be desirable. By increasing complexity in the encoder, you may be able to significantly reduce complexity in the decoders and thus reduce the cost of the consumer reception or playback device.
Transforms
Transforms manipulate image data in ways that make it easier to separate the important from the unimportant. Three types are currently used for video compression: Wavelets, , and the Discrete Cosine Transform or DCT.
Wavelets--The Wavelet transform employs a succession of mathematical operations that can be thought of as filters that decompose an image into a series of frequency bands. Each band can then be treated differently depending on its visual impact. Since the most visually important information is typically concentrated in the lowest frequencies in the image or in a particular band, they can be coded with more bits than the higher ones. For a given application, data can be reduced by selecting how many bands will be transmitted, how coarsely each will be coded and how much error protection each will receive.
The wavelet technique has advantages in that it is computationally simpler than DCT and easily scalable. The same compressed data file can be scaled to different compression ratios simply by discarding some of it prior to transmission.
The study of wavelets has lagged about 10 years behind that of DTC, but it is now the subject of intensive research and development. A Wavelet algorithm has been chosen for coding still images and textures in MPEG-4, and another is the basis for the new JPEG-2000 still image standard for which final approval is expected in 2001 (ISO 15444). More applications are likely in the future.
Fractals--The fractal transform is also an intra-frame method. It is based on a set of two dimensional patterns discovered by Benoit Mandelbrot at IBM. The idea is that you can recreate any image simply by selecting patterns from the set and then appropriately sizing, rotating and fitting them into the frame (see figure 1). Rather than transmitting all the data necessary to recreate an image, a fractal coder relies on the pattern set stored in the decoder and sends only information on which patterns to use and how to size and position them.
The fractal transform can achieve very high compression ratios and is used extensively for sending images on the Internet. Unfortunately, the process of analyzing original images requires so much computing power that fractals aren't feasible for realtime video. The technique also has difficulties with hard-edged artificial shapes such as character graphics and buildings. It works best with natural objects like leaves, faces and landscapes.
DCT--The discrete cosine transform is by far the most used transform in video compression. It's found in both intra-frame and inter-frame systems, and it's the basis for JPEG, MPEG, DV and the H.xxx videoconferencing standards.
Like wavelets, DCT is based on the theory that the eye is most sensitive to certain two-dimensional frequencies in an image and much less sensitive to others.
With DCT, the picture is divided into small blocks, usually 8 pixels by 8 pixels. The DCT algorithm converts the 64 values that represent the amplitude of each of the pixels in a block into 64 new values (coefficients) that represent how much of each of the 64 frequencies are present.
At this point, no compression has taken place. We've traded one batch of 64 numbers for another and we can losslessly reverse the process and get back to our amplitude numbers if we choose--all we did was call those numbers something else.
Since most of the information in a scene is concentrated in a few of the lower-frequency coefficients, there will be a large number of coefficients that have a zero value or are very close to zero. These can be rounded off to zero with little visual effect when pixel values are reconstituted by an inverse DCT process in the decoder.
The Importance Of Standards
The almost universal popularity of DCT illustrates the power of a standard. DCT may not be the best transform, but once a standard (either de facto or de jure) is in wide use, it will be around for a long time. Both equipment-makers and their customers need stability in the technologies they use, mainly so they can reap the benefits of their investments. The presence of a widely accepted standard provides that stability and raises the performance bar for other technologies that would like to compete. To displace an accepted standard, the competitor can't just be better, it must be several orders of magnitude better (and less expensive won't hurt either).
The incorporation of DCT techniques in the JPEG and MPEG standards and subsequent investment in and deployment of DCT--based compression systems have ensured its dominance in the compression field for a long time to come.
M-JPEG--JPEG, named for the Joint Photographic Experts Group, was developed as a standard for compressing still photographic images. Since JPEG chips were readily available before other compression chip sets, designers who wanted to squeeze moving pictures into products such as computer-based nonlinear editing systems adapted the JPEG standard to compress strings of video frames. Motion-JPEG was born.
Unfortunately, the JPEG standard had no provision for storing the data related to motion, and designers developed their own proprietary ways of dealing with it. Consequently, it's often difficult to exchange M-JPEG files between systems.
Not long after the JPEG committee demonstrated success with still images, the Motion Picture Experts Group (MPEG) and DV standardization committees developed compression standards specifically for moving images. The trend has been for these newer motion standards to replace proprietary M-JPEG approaches.
A new JPEG-2000 still image standard using wavelet compression is being finalized. An extension of this standard (expected in 2001) may include a place to store data specifying the order and speed at which JPEG-2000 frames can be sequenced for display. This feature is designed to accommodate rapid sequence, digital still cameras and is not intended to compete with MPEG, however, it's conceivable that a new, standardized motion JPEG could emerge.
DV--The DV compression format was developed by a consortium of more than 50 equipment manufacturers as a consumer digital video cassette recording format (DVC) for both standard and high definition home recording. It is an intra-frame, DCT-based, symmetrical system.
Although designed originally for home use, the inexpensive DV compression engine chip set (which can function as either encoder or decoder) has proved itself versatile enough to form the basis for a number of professional products including D9, DVCAM and DVCPRO. Both D9 and DVCPRO have taken advantage of the chipset's scalability to increase quality beyond that available in the consumer product.
At 25 Mbps, the consumer compression ratio is about 5:1 with 4:1:1 color sampling. D9 and DVCPRO50 use two of the mass-market compression circuits running in parallel to achieve a 3.3:1 compression ratio with 4:2:2 color sampling at 50 Mbps. DVCPROHD and D9HD (scheduled to debut in 2000) are technically capable of recording progressive scan standard definition or interlaced and progressive HDTV at 100 Mbps. Similar extensions are possible beyond 100 Mbps and DV compression is not limited to video cassette recording, but can be applied to a range of compressed digital video storage and transmission applications.
MPEG--MPEG has become the 800--pound gorilla of compression techniques. It is the accepted compression scheme for all sorts of new products and services, from satellite broadcasting to DVD to the new ATSC digital television transmission standard, which includes HDTV.
MPEG is an asymmetrical, DCT compression scheme which makes use of both intra- and inter-frame, motion compensated techniques.
One of the important things to note about MPEG is that it's not the kind of rigidly defined, single entity we've been used to with NTSC or PAL, or the ITU-R 601 digital component standard.
MPEG only defines bit streams and how those streams are to be recognized by decoders and reconstituted into video, audio and other usable information. How the MPEG bit streams are encoded is undefined and left open for continuous innovation and improvement.
You'll notice we've been referring to MPEG bit streams in the plural. MPEG isn't a single standard, but rather a collection of standardized compression tools that can be combined as needs dictate. MPEG-1 provided a set of tools designed to record video on CDs at a data rate around 1.5 Mbps. While that work was underway, researchers recognized that similar compression techniques would be useful in all sorts of other applications.
The MPEG-2 committee was formed to expand the idea. They understood that a universal compression system capable of meeting the requirements of every application was an unrealistic goal. Not every use needed or could afford all the compression tools that were available. The solution was to provide a series of Profiles and Levels (see figure 2) with an arranged degree of commonality and compatibility between them.
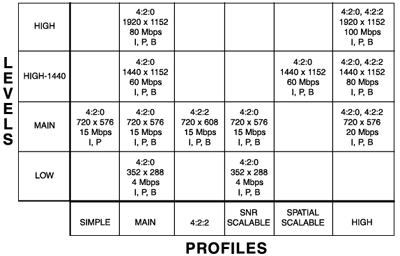
Profiles And Levels--The six MPEG-2 Profiles gather together different sets of compression tools into toolkits for different applications. The Levels accommodate four different grades of input video ranging from a limited definition similar to today's consumer equipment all the way to high definition.
Though they organized the options better, the levels and profiles still provided too many possible combinations to be practical. So, the choices were further constrained to specific "compliance points" within the overall matrix. So far, 12 compliance points have been defined ranging from the Simple Profile at Main Level (SP@ML) to the High Profile at High Level (HP@HL). The Main Profile at Main Level (MP@ML) is supposed to approximate today's broadcast video quality.
Any decoder that is certified at a given compliance point must be able to recognize and decode not only that point's set of tools and video resolutions, but also the tools and resolutions used at other compliance points below it and to the left. Therefore, an MP@ML decoder must also decode SP@ML and MP@LL. Likewise, a compliant MP@HL decoder would have to decode MP@H14L (a compromise 1440x1080 pixel HDTV format), MP@ML, MP@LL and SP@ML.
As with MP@H14L, not all of the defined compliance points have found practical use. By far the most common is MP@ML. The proposed broadcast HDTV systems fall within the MP@HL point.
Group Of Pictures--MPEG achieves both good quality and high compression ratios at least in part through its unique frame structure referred to as the "Group of Pictures" or Gop (see figure 3). Three types of frames are employed: 1) intra-coded or "I" frames; 2) predicted "P" frames which are forecast from the previous I or P frame; and 3) "B" frames, which are predicted bidirectionally from both the previous and succeeding I or P frames. A GoP may consist of a single I frame, an I frame followed by a number of P frames, or an I frame followed by a mixture of B and P frames. A GoP ends when the next I frame comes along and starts a new GoP.
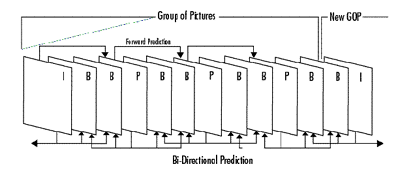
All the information necessary to reconstruct a single frame of video is contained in an I frame. It uses the most bits and can be decoded on its own without reference to any other frames. There is a limit to the number of frames that can be predicted from another. The inevitable transmission errors and small prediction errors will add up and eventually become intolerable. The arrival of a new I frame refreshes the process, terminates any accumulated errors and allows a new string of predictions to begin.
P frames require far fewer bits because they are predicted from the previous I frame. They depend on the decoder having the I frame in memory for reference.
Even fewer bits are needed for B frames because they are predicted from both the preceding and following I or P frames, both of which must be in memory in the decoder. The bidirectional prediction of B frames not only saves lots of bits, it also makes it possible to simulate VCR search modes.
The Simple Profile does not include B frames in its toolkit, thus reducing memory requirements and cost in the decoder. All other profiles include B frames as a possibility. As with all MPEG tools, the use, number and order of I, B and P frames is up to the designer of the encoder. The only requirement is that a compliant decoder be able to recognize and decode them if they are used.
In practice, other standards that incorporate MPEG such as DVB and ATSC may place further constraints on the possibilities within a particular MPEG compliance point to lower the cost of consumer products.
Compression Ratio Versus Picture Quality
Because of its unique and flexible arrangement of I, P and B frames, there is little correlation between compression ratio and picture quality in MPEG. High qual-
ity can be achieved at low bit rates with a long GoP (usually on the order of 12 to 16 frames). Conversely, the same bit rate with a shorter GoP and/or no B frames will produce a lower quality image.
Knowing only one or two parameters is never enough when you're trying to guess the relative performance of two different flavors of MPEG.
4:2:2 Profile
As MPEG-2 field experience began to accumulate, it became apparent that, while MP@ML was very good for distributing video, it had shortcomings for post production. The 720x480 and 720x526 sampling structures defined for the Main Level ignored the fact that there are usually 486 active picture lines in 525-line NTSC video and 575 in 625-line PAL.
With the possible exception of cut transitions and limited overlays, lossy compressed video cannot be post-processed (resized, zoomed, rotated) in its compressed state. It must first be decoded to some baseband form such as ITU-R 601. Without specialized decoders and encoders designed to exchange information about previous compression operations, the quality of MP@ML deteriorates rapidly when its 4:2:0 color sampling structure is repeatedly decoded and re-encoded during post production.
Long GoPs, with each frame heavily dependent on others in the group, make editing complex and difficult. And, the MP@ML 15 Mbps upper data rate limit makes it impossible to achieve good quality with a short GoP of one or two frames.
Alternative intra-frame compression techniques such as DV and Motion-JPEG were available. But many people thought that if the MPEG MP@ML shortcomings could be corrected, the basic MPEG tools would be very useful for compressing contribution-quality video down to bit rates compatible with standard telecom circuits and inexpensive disk stores. And so they created a new Profile.
As its name suggests, the 4:2:2 Profile (422P@ML) uses 4:2:2 color sampling which more readily survives re-encoding. The maximum number of video lines is raised to 608. And the maximum data rate is increased to 50 Mbps.
Noting the success of the new profile for standard definition images, the Society of Motion Picture and Television Engineers used MPEG's 422P@ML as a foundation for SMPTE-308M, a compression standard for contribution quality high definition. It uses the MPEG tools and syntax to compress HDTV at data rates up to 300 Mbps.
SMPTE submitted 308M to MPEG to help guide their work on a high level version of 422P. The documents for MPEG 422P@HL have been completed. The two standards are independent, but fully interoperable. The principal difference is that SMPTE 308M specifies an encoder constraint, requiring a staircase relationship between GoP and bitrate. Longer GoPs are permitted only at lower bitrates. MPEG places no restrictions on encoders and any combination of bitrate and GoP is permissible.
MPEG-4
With work on MPEG-1 and MPEG-2 complete, the Experts Group turned its attention to the problems posed by interactive multimedia creation and distribution. MPEG-4 is the result. It is not intended to replace MPEG 1 or 2, but, rather, builds on them to foster interactivity. Like MPEG-2, it is a collection of tools that can be grouped into profiles and levels for different applications. Version one of the MPEG-4 standard is already complete, and the ink is drying fast on version two.
In committee jargon, MPEG-4 provides a Delivery Multimedia Integration Framework (DMIF) for "universal access" and "content-based interactivity." Translated, that means the new toolkit will let multimedia authors and users store, access, manipulate and present audio/visual data in ways that suit their individual needs at the moment, without concern for the underlying technicalities.
It's a tall order. If accepted in practice, MPEG-4 could resolve the potentially unmanageable tangle of proprietary approaches we've seen for audio and video coding in computing, on the internet and in emerging wireless multimedia applications. Toward that end, it borrows from videoconferencing standards and expands on the previous MPEG work to enhance performance in low bitrate environments and provide the tools necessary for interactivity and intellectual property management.
What really sets MPEG-4 apart are its tools for interactivity. Central to these is the ability to separately code visual and aural "objects." Not only does it code conventional rectangular images and mono or multi-channel sound, but it has an extended set of tools to code separate audio objects and arbitrarily shaped video objects.
A news anchor might be coded separately from the static background set. Game pieces can be coded independently from their backgrounds. Sounds can be interactively located in space. Once video, graphic, text or audio objects have been discretely coded, users can interact with them individually. Objects can be added and subtracted, moved around and re-sized within the scene.
All these features are organized by a DIMF that manages the multiple data streams, two-way communication and control necessary for interaction.
Both real and synthetic objects are supported. There are MPEG-4 tools for coding 2D and 3D animations and mapping synthetic and/or real textures onto them. Special tools facilitate facial and body animation. Elsewhere in the toolkit are methods for text-to-speech conversion and several levels of synthesized sound.
A coordinate system is provided to position objects in relation to each other, their backgrounds and the viewer/listener. MPEG-4's scene composition capabilities have been heavily influenced by prior work done in the Internet community on the Virtual Reality Modeling Language (VRML), and there is formal coordination between MPEG and the Web3d Consortium to insure that VRML and MPEG-4 evolve in a consistent manner.
Unlike VRML, which relies on text-based instructions, MPEG- 4's scene description language, Binary Format for Scenes (BIFS), is designed for real-time streaming. Its binary code is 10 to 15 times more compact than VRML's, and images can be constructed on the fly without waiting for the full scene to download.
Coding and manipulating arbitrarily shaped objects is one thing. Extracting them from natural scenes is quite another. Thus far, MPEG-4 demonstrations have depended on chromakey and a lot of hand work.
In version 2, programming capabilities will be added with MPEG-J, a subset of the Java programming language. Java interfaces to MPEG-4 objects will allow decoders to intelligently and automatically scale content to fit their particular capabilities.
The standard supports scalability in many ways. Less important objects can be omitted or transmitted with less error protection. Visual and aural objects can be created with a simple layer that contains enough basic information for low resolution decoders and one or more enhancement layers that, when added to that base layer, provide more resolution, wider frequency range, surround sound or 3D.
MPEG-4's basic transform is still DCT and quite similar to MPEG 1 and 2, but improvements have been made in coding efficiency and transmission ruggedness. A wavelet algorithm is included for efficient coding of textures and still images. MPEG-4 coding starts with a Very Low Bitrate Video (VLBV) core, which includes algorithms and tools for data rates between 5 kbps and 64 kbps. To make things work at these very low bit rates, motion compensation, error correction and concealment have been improved, refresh rates are kept low (between 0 and 15 fps) and resolution ranges from a few pixels per line up to CIF (352x288).
MPEG-4 doesn't concern itself directly with the error protection needed in specific channels such as cellular radio, but it has made improvements in the way payload bits are arranged so that recovery will be more robust. There are more frequent resynchronization markers. New, reversible variable length codes can be read forward or backward like a palindrome so decoders can recover all the data between an error and the next sync marker.
For better channels (something between 64 kbps and 2 Mbps), a High Bitrate Video (HBV) mode supports resolutions and frame rates up to Rec.601. The tools and algorithms are essentially the same as VLBV, plus a few additional ones to handle interlaced sources.
While MPEG-4 has many obvious advantages for interactive media production and dissemination, it's not clear what effect it will have on conventional video broadcasting and distribution. MPEG-2 standards are well established in these areas. For the advanced functions, both MPEG-4 encoders and decoders will be more complex and, presumably, more expensive than those for MPEG-1 and 2. However, the Studio Profile of MPEG-4 is expected to have an impact on high-end, high-resolution production for film and video.
MPEG-4 STUDIO PROFILE
At first glance, MPEG-4's bandwidth efficiency, interactivity and synthetic coding seem to have little to do with high resolution, high performance studio imaging. The MPEG-4 committee structure did, however, provide a venue for interested companies and individuals to address some of the problems of high-end image compression.
When you consider realtime electronic manipulation of high resolution moving images, the baseband numbers are enormous. A 4000 pixel by 4000 pixel, 4:4:4, YUV/RGB, 10-bit, 24 fps image with a key channel requires a data rate in excess of 16 Gbps. Even the current HDTV goal (just out of reach) of 1920x1080 pixels, 60 progressive frames and 4:2:2, 10-bit sampling requires just under 2.5 Gbps. Upgrade that to 4:4:4 RGB, add a key channel and you're up to about 5 Gbps. It's easy to see why standards for compressing this stuff might be useful.
The MPEG-4 committee was receptive to the idea of a Studio Profile, and their structure provided an opportunity to break the MPEG-2 upper limits of 8-bit sampling and 100 Mbps data rate. The project gathered momentum as numerous participants from throughout the imaging community joined in the work. Final standards documents are expected by the end of 2000.
A look at the accompanying table shows three levels in the proposed new profile. Compressed data rates range between 300 Mbps and 2.5 Gbps. With the exception of 10-bit sampling, the Low Level is compatible with and roughly equivalent to the current MPEG-2 Studio Profile at High Level.
The Main Level accommodates up to 60 frames progressive, 4:4:4 sampling, and 2048x2048 pixels. The High Level pushes things to 12-bit sampling, 4096x4096 pixels and up to 120 frames per second. The draft standard is expected to include provisions for key channels, although the number of bits for them were still in question as of this writing.
Although you can't have everything at once (a 12-bit, 120 fps, 4:4:4:4, 4096x4096 image isn't in the cards), within a level's compressed data rate limitations, you can trade resolution, frame rate, quantizing and sampling strategies to accomplish the task at hand.
Like all MPEG standards, this one defines a bitstream syntax and sets parameters for decoder performance. For instance, a compliant High Level decoder could reproduce a 4096x4096 image at 24 frames per second or a 1920x1080 one at 120 fps. At the Main Level, a 1920x1080 image could have as many as 60 fames per second where a 2048x2048 one would be limited to a maximum of 30 fps.
As a part of MPEG-4, the Studio Profile could use all the scene composition and interactive tools that are included in the lower profiles. But high-end production already has a large number of sophisticated tools for image composition and manipulation, and it's not clear how or if similar components of the MPEG-4 toolkit will be applied to the Studio Profile.
One side benefit of a Studio Profile in the MPEG-4 standard is that basic elements such as colorimetry, macroblock alignments and other parameters will be maintained all the way up and down the chain. That should help maintain quality as the material passes from the highest levels of production all the way down to those Dick Tracy wrist receivers.
THE OTHER MPEGs
MPEG 7 and 21 are, thankfully, not new compression standards, but rather attempts to manage motion imaging and multimedia technology.
MPEG-7 is described as a Multimedia Content Description Interface (MCDI). It's an attempt to provide a standard means of describing multimedia content. Its quest is to build a standard set of descriptors, description schemes and a standardized language that can be used to describe multimedia information. Unlike today's text-based approaches, such a language might let you search for scenes by the colors and textures they contain or the action that occurs in them. You could play a few notes on a keyboard or enter a sample of a singer's voice and get back a list of similar musical pieces and performances.
If the MPEG-7 committee is successful, search engines will have at least a fighting chance of finding the needles we want in the haystack of audio visual material we're creating. A completed standard is expected in September 2000.
MPEG-21 is the Group's attempt to get a handle on the overall topic of content delivery. By defining a Multimedia Framework from the viewpoint of the consumer, they hope to understand how various components relate to each other and where gaps in the infrastructure might benefit from new standards.
The subjects being investigated overlap and interact. There are network issues like speed, reliability, delay, cost performance and so on. Content quality issues include things such as authenticity (is it what it pretends to be?) and timeliness (can you have it when you want it?), as well as technical and artistic attributes.
Ease of use, payment models, search techniques and storage options are all part of the study, as are the areas of consumer rights and privacy. What rights do consumers have to use, copy and pass on content to others? Can they understand those rights? How will consumers protect personal data and can they negotiate privacy with content providers? A technical report on the MPEG-21 framework is scheduled for mid-2000.
THE MISSING MPEGs
Since we've discussed MPEG 1, 2, 4, 7 and 21, you might wonder what happened to 3, 5, 6 and the rest of the numbers. MPEG-3 was going to be the standard for HDTV. But early on, it became obvious that MPEG-2 would be capable of handling high definition and MPEG-3 was scrapped.
When it came time to pick a number for some new work to follow MPEG-4, there was much speculation about what it would be. (Numbering discussions in standards work are like debates about table shape in diplomacy. They give you something to do while you're trying to get a handle on the serious business.) With one, two and four already in the works, the MPEG folks were on their way to a nice binary sequence. Should the next one be eight, or should it just be five? In the end, they threw logic to the winds and called it seven. Don't even ask where 21 came from (the century perhaps?).
Some Final Thoughts
Use clean sources. Compression systems work best with clean source material. Noisy signals, film grain, poorly decoded composite video--all give poor results. Preprocessing that reduces noise, shapes the video bandwidth and corrects other problems can improve compression results, but the best bet is a clean source to begin with. Noisy and degraded images can require a premium of 20 to 50 percent more bits.
Milder is better. Video compression has always been with us. (Interlace is a compression technique. 4:2:2 color sampling is a compression technique.) It will always be with us. Nonetheless, you should choose the mildest compression you can afford in any application, particularly in post production where video will go through multiple processing generations.
Compression schemes using low bit rates and extensive inter-frame processing are best suited to final program distribution.
More is better. Despite the fact that there is only a tenuous relationship between data rate and picture quality, more bits are usually better. Lab results suggest that if you acquire material at a low rate such as 25 Mbps and you'll be posting it on a nonlinear system using the same type of compression, the multigeneration performance will be much better if your posting data rate is higher, say 50 Mbps, than if you stay at the 25 Mbps rate.
Avoid compression cascades. When compressed video is decoded, small errors in the form of unwanted high frequencies are introduced where no high frequencies were present in the original. If that video is re-encoded without processing (level changes, zooming, rotation, repositioning) and with the same compression scheme, the coding will usually mask these errors and the effect will be minimal. But if the video is processed or re-encoded with a different compression scheme, those high frequencies end up in new locations and the coding system will treat them as new information. The result is an additional loss in quality roughly equal to that experienced when the video was first compressed. Re-coding quality can be significantly improved by passing original coding parameters (motion vectors, quantization tables, frame sequences, etc.) between the decoder and subsequent encoder. Cascades between different transforms (i.e. from DCT based compression to Wavelets and vice versa) seem to be more destructive than cascades using the same transform. Since Murphy's Law is always in effect, these losses never seem to cancel each other, but add rapidly as post production generations accumulate.
Quality is subjective. Despite recent advances in objective measures, video quality in any given compression system is highly dependent on the source material. Beware of demonstrations that use carefully selected material to achieve low bit rates. Be sure to see what things look like with your own test material covering the range of difficulty you expect in daily operation.
Bandwidth based on format. The total ATSC bandwidth is 19.39 Mbps, which includes audio, video and other data. As the image quality is increased, more bandwidth is needed to send the image, even though it is compressed. Below is a list of popular distribution formats and the approximate bandwidth they will require (30 fps for interlace, 60 fps for progressive).
1080i: 10 to 18 Mbps (10 with easy clean film material, easy clean video material may be a little higher, sports will require 18, all material will require 18 on some of the earlier encoders).
720p: 6 to 16 Mbps (low numbers with talking heads and films, sports may be acceptable under 16 Mbps).
480p: 4 to 10 Mbps (low number highly dependent on customer expectation that this a very high quality 16:9 image).
480i: 2 to 6 Mbps (could average under 3 Mbps with good statistical multiplexing).
Things will go wrong. You can count on it. When they go wrong in digital recording and transmission, bits are corrupted and the message is distorted. The effect of these distortions varies with the nature of the digital system.
With computers, there is a huge sensitivity to errors, particularly in instructions. A single error in the right place and it's time to reboot. With video and audio the effect is more subjective.
If a single video or audio bit has been corrupted, the effect depends on the significance of that bit. If it's the least significant bit in a sample, chances are the effect will be lost in the noise and won't even be noticed. If it's one of the more significant bits, there will probably be a pop in the sound or an unwanted dot in the picture. If the error occurs in a sync word, you could lose a whole line or frame. With compressed video, an error in just the right place could disrupt not only one frame but a long string of frames.
Causes Of Error
There are lots of reasons why errors occur. The error environment inside a piece of equipment is usually pretty benign. Manufacturers can control noise, crosstalk and other potential interference so that, for all intents and purposes, there will be no errors. Broadcast channels, on the other hand, can be downright hostile. There is all sorts of noise caused by everything from circuitry to lightning to your neighbor's power tools.
Magnetic recording provides lots of opportunity for mischief, too. Small random errors can affect single bits, and isolated large bursts of errors can disrupt a whole array of bits in an area that is otherwise error-free. Errors can be caused by random noise in heads and replay circuits, or losses of head-to-tape contact resulting from imperfections in the magnetic coating, small bits of dust from the media itself and/or improper storage and handling (that unboxed cassette that's been lying in a bag of fries on the dashboard of the news truck all day).
Even an environment as seemingly safe as the inside of a memory chip can have problems. The tiny wells of capacitive charge that represent zeros and ones can be discharged by alpha particles from the natural radioactive decay of the chip's own materials. Statistically this is only going to happen once every 30 years or so, but with thousands of chips in a large memory bank, the probability rises to an error every few minutes.
Every digital channel has its own set of problems, and the solutions applied will be different for each type of channel. There are, however, four broad stages common to all error management schemes:
Error Avoidance And Redundancy Coding--The first steps in error management constitute a sort of preprocessing in anticipation of the errors to come. Much of this is simply good engineering, doing as much as we can to avoid errors. We design circuitry to minimize noise and crosstalk. We find bad spots on hard discs and lock them out. We see to it that there is enough transmit power and a good enough antenna to ensure an adequate signal--to--noise ratio at the receiver. We keep the cassette out of the fries and off the dashboard.
Error Detection--Next comes some really clever engineering called "redundancy coding." Without it, error detection would be impossible. Detection is one of the most important steps in error management. It must be very reliable. If you don't know there has been an error, it doesn't matter how effective your other error management techniques are.
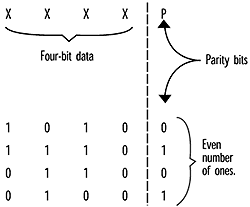
Redundancy codes can be extremely complex, but we can use a very simple one, the parity check, to explain the idea. Like all redundancy codes, the parity check adds bits to the original data in such a way that errors can be recognized at the receiver. Consider the example in figure 4. Here we have a series of four-bit data words to which a fifth "parity" bit has been added. By adding a zero or a one, the parity bit ensures that there will be an even number of ones in all the coded data words. If the error detection circuitry in the receiver sees an odd number of ones, it knows an error has taken place.
Error Correction--In our simple parity example, when the receiver sees an odd number of ones, it knows that an error has occurred in one of the four-bit data bits. But it doesn't know which bit is wrong. The error can be corrected by asking for a retransmission of the corrupted data word.
Retransmission requests are commonly used to correct errors in computing, but they're a luxury we can't afford with realtime video and audio. We need the bits when we need them, and we can't interrupt the flow for a retry. We need a scheme that can correct errors.
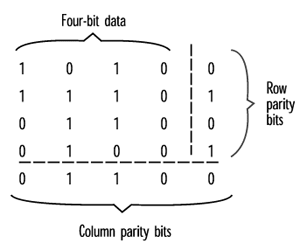
A "crossword parity check" is a simple example of a redundancy code that can identify which bit is corrupted so that it can be fixed. In figure 5, parity bits are added to both rows and columns. If a single bit is distorted, one row check and one column check will fail (an odd number of ones again) and the bad bit will be at the intersection of the column and row. If there's a one in the corrupted location, it can be corrected to a zero and vice versa.
Unfortunately, any scheme has a finite number of errors it can correct. Closely spaced bursts of errors are a common occurrence, and a burst can screw up more data than even the best coding can fix. Sometimes data can be interleaved during transmission or recording to improve a system's chances in the face of such bursts.
Consider an error correction scheme that can only correct up to four bad data words in a row. It must work in a channel where six--word error bursts are common. What happens if we change the order of our data words so that adjacent words in the original data are no longer adjacent in the transmission channel? Error bursts will still affect six adjacent words in the channel, but when those words are put back into their original order at the other end, it's unlikely that there will be four bad words in a row and the correction scheme can correct the errors.
Error Concealment--No matter how elegant the coding, errors will occur that cannot be corrected. The only option is to conceal them as best we can.
One example of error concealment is the dropout compensation used in analog video recorders. During playback, when a dropout is detected, the dropout compensator inserts some video from the previous line into the hole created by the loss of signal. Since adjacent lines usually contain similar video, the idea works fairly well.
That basic idea has been refined and improved in digital systems. With digital audio, the simple fix is to approximate a lost sample by interpolating a value from samples on either side. A more advanced method makes a spectral analysis of the sound and inserts samples with the same spectral characteristics. If there are too many errors to conceal, then the only choice is to mute.
With digital video, missing samples can be approximated from adjacent ones in the same line, those on adjacent lines and/or ones in previous and succeeding fields. The technique works because there is a lot of redundancy in a video image. If the video is compressed, there will be less redundancy, concealment may not work as well, and error correction will become even more important.
In any case, when both correction and concealment capabilities are exceeded in video, the options are to either freeze the last frame or drop to black.
Concealment techniques aren't limited to recording and transmission. They're even being used in cameras. Thomson's 1657D digital camera uses it to correct defective CCD pixels. Although defective pixels are rare, they do occur, and the Thomson Dynamic Pixel Correction system continuously analyzes the image, detects bad pixels and automatically interpolates a new value for them from surrounding pixels in realtime.
Tradeoffs
It can be argued that, since redundancy codes add bits to the stream, they reduce storage capacity or channel bandwidth. That's not true if they're properly designed for the channel in question.
Consider magnetic recording. With a properly designed redundancy code, the signal-to-noise ratio of the channel can be reduced because an increased number of errors can be overcome by the error correction system. Cutting track width in half will reduce signal-to-noise ratio by 3 dB, but it doubles storage capacity. With the doubled capacity, it's not difficult to accommodate the extra bits added by the correction scheme.
A properly designed error management system is always worth much more than the bits it consumes.
To understand the emerging world of digital television, one must let go of preconceptions rooted in the history of analog television. A world where the image acquisition, transmission, and consumer display components of the broadcast system are tightly coupled. A world where one size fits all.
The NTSC transmission standard was designed to deliver a resolution of approximately 21 cycles per degree (cpd) over a viewing field of just under 11 degrees--a resolution of 22 cpd is considered to be a sharp image for people with average visual acuity. In studies where viewers are shown video images on displays with varying sizes and resolutions, and are given the opportunity to select a preferred viewing distance, they will typically choose the distance that produces a sharp image.
In order to deliver the NTSC viewing experience, the engineers who designed the standard assumed that we would watch a 19-inch diagonal display at an average viewing distance of seven picture heights, a distance of about six to seven feet. If we increase the size of the display, to cover a larger portion of the field of view, the limitations of the NTSC standard quickly become apparent. In reality, the NTSC one-size-fits-all approach only delivers a sharp image when the display covers less than 11 degrees of the field of view.
Theater screens typically cover a 30- to 50-degree field of view; special venue theaters such as Imax may cover a 180-degree field of view. The move to high resolution electronic imaging systems deals, in large measure, with the ability to cover a significantly greater portion of the field-of-view, with what is perceived as a sharp and accurate image.
In order for digital television to satisfy the desired goal of screens that cover a larger portion of the field of view, we need to deliver more information to the viewer, not more resolution. It's better to think of the requirements for larger displays in the same terms as a picture window in the family room. If we make the window larger, we get to see more of the back yard; the resolution remains constant.
The DTV display in the family room should do the same, providing a sharp image at the designed viewing distance for the installation. Thus, the choice of an appropriate level of resolution for a consumer display will depend on the viewing environment (the application) and the available budget.
In the emerging digital world, acquisition, transmission and display are not connected. Images will be captured at many spatial resolutions (size) and temporal rates (images per second, both interlace and progressive). Content will be composed by intermixing visual objects from many sources, and it will be encoded for distribution at many levels of resolution. Ultimately, the content will be decoded and scaled for presentation on screens that come in many sizes and resolutions.
While digital television provides an appropriate technical foundation for a system without rigid video formats--i.e., resolution independence--it's more practical to design the system with several levels of resolution in a logical progression. This is the approach taken by the engineers who designed the ATSC digital television standard; the number of lines increases by a factor of 1.5 between each level.
Figure 6: The Sharper Image, and figure 7: Sm., Med., Lg., provide a visual framework to assist with your understanding of how the ATSC formats can be used to deliver the DTV viewing experience.
This bewildering array of possibilities takes digital video and broadcasting into an entirely new realm. A world where the digitized representations of all forms of media can be encoded for delivery as streams of packetized data. When these digital bit streams are decoded, images will be scaled for presentation to match the requirements of the viewing application and the resolution of the digital television appliance where the content is being consumed--the TV set in the family room or the den, the direct view CRT or LCD screens of personal computers, or the next generation of network computers and home theater systems with large projection screens, or plasma displays that hang on the wall.
To understand digital television, it is helpful to understand the ways in which the human visual and auditory systems acquire images and sound. From this, we can better understand the analog and digital processes that are being carefully tuned to emulate the way we see and hear. These processes are intimately related to the way we will sample images and sound, and compress this data for delivery using digital transmission techniques.
 figure 6. The Sharper Image How much resolution does a television system need to produce a sharp image? The level of resolution required to deliver a sharp image is directly related to the size of the screen and the viewing distance. When viewed from the designed viewing distance of seven picture heights, NTSC appears sharp. Step closer, say three picture heights, and you will see the limitations of the NTSC standard. The ATSC standard supports three levels of spatial resolution for the transmission of 16:9 images, as illustrated above. This image has been carefully constructed to illustrate the relative resolution of the three format families, using frame based image sampling (progressive scan). It does not reflect the loss of vertical resolution that results from interlaced image sampling or display. If you have average visual ability, this simple test will demonstrate the relationship between resolution and viewing distance. If this image is viewed from three picture heights --about eight inches--1920x1080 should appear sharp; you should be able to see the samples in the 704x480 image and steps on the curves in the 1280x720 image. At five picture heights--about 13 inches--1280x720 should appear sharp; and at seven picture heights--about 19 inches--704x480 should appear sharp. |
In the physical world, what we see and what we hear are analog in nature. Sound is a continuous phenomenon, the result of the modulation of our ear drums by moving air molecules. Sight is a continuous phenomenon, the result of a continuous flow of photons into the receptors of the human visual system. How we see and hear is the basis for how visual and aural data can be compressed--with parts of that information "thrown away."
The human visual system relies on multiple image receptors to deal with the diversity of environments that it encounters: cones are utilized for color image acquisition over a wide range of illumination levels; rods are utilized for monochrome image acquisition at low illumination levels.
The cones are organized into three broad groups of receptors that are sensitive to light in specific spectral bands; while these bands have significant overlaps, they roughly conform to the red, green and blue portions of the spectrum. Red and green receptors each outnumber blue receptors by a factor of 2:1. The disbursement of these receptors is not uniform; thus, spatial perception deals with a complex matrix of receptor types and cognitive processing by the brain.
The center of the visual field, an area called the fovea, contains 30,000 to 40,000 cones (no rods). Central vision enables us to see detail, while peripheral vision is tuned to detect change, i.e., temporal events.
It takes several hundred milliseconds for the foveal image receptors to capture a detailed image; thus the eye must either be viewing a static scene or it must track a moving object to perceive high resolution.
Evidence suggests the massive amount of information collected by our visual and auditory sensors is digitized and processed by the brain, allowing us to discriminate among content of interest and content that can be ignored. In essence we learn how to filter the input from the physical world--to see and hear in a very selective manner.
 figure 7. Sm. Med. Lg. Television displays already come in many sizes; now we are adding a confusing new variable to the buying decision--display resolution. As you saw in figure 6, viewing distance determines the resolution requirements for a display, regardless of its size. The goal is to deliver a sharp image--approximately 22 cycles per degree of field of view--at the intended viewing distance. This figure illustrates how resolution requirements increase with the field of view covered by the display. Imagine that the numbers above represent pieces of three screens, all in the same plane (equal distance between viewer and screens). The numbers are all the same height, when the measurement is expressed as a percentage of total picture height. The width and height of the 720--line display is 1.5 that of the 480--line display; in turn, the width and height of the 1080--line display is 1.5 times that of 720--line display. Under these conditions, as in this illustration, the size of the samples presented to the observer are equal, thus the displays should deliver equivalent perceived sharpness. How should you choose a DTV display? Measure the space for the display and the average viewing distance. When shopping, look at displays that fit the space and your budget, then judge image quality at the intended viewing distance. |
The image compression techniques that enabled the first six decades of analog television broadcasting provided limited control over the process of selecting which information to keep, and which information to throw away.
With digital television, we can tweak the system in new ways. We can be more selective about the information we throw away and the important bits we pass along to the human visual and auditory systems.
Conserving Bandwidth In An Analog World
Like the sensors of the human visual system, a television camera produces an abundance of information. Today's interlaced, broadcast-quality cameras typically employ three CCD sensors, producing red, green and blue outputs, each with 6 to 8 MHz of analog information. Unfortunately, stuffing 18 to 24 MHz of analog signals into a 6 MHz NTSC, or 8 MHz PAL channel was a bit tricky at the time these standards were created. The engineers who designed analog television had to throw away a great deal of information.
NTSC and PAL are analog video compression systems, designed to deliver a reasonable balance between static and dynamic resolution. The approximate 3:1 compression is achieved primarily by limiting color resolution and high frequency luminance detail.
The RGB signals are added in a mathematical matrix to produce full bandwidth luminance and color difference signals. These signals are then filtered, limiting the luminance (Y) frequency response to approximately 4.2 MHz in NTSC and 6.0 MHz in PAL. The color or chroma difference signals (I and Q for NTSC, U and V for PAL) are filtered more aggressively, leaving only 1.5 MHz for I and 0.5 MHz for Q in NTSC, 1.5 MHz for U and V in PAL. Thus, color resolution is reduced to approximately one-quarter of the luminance resolution.
Unlike film, where a light source passes through a complete image frame, projecting the image onto a screen, television systems must deliver images as part of a continuously modulated signal that can be decoded by an inexpensive television appliance.
In the early part of this century, when our analog television systems were designed, the technology was not available to store and then display a complete image frame. The solution was to deliver the images using line scanning techniques, synchronized with the modulated television signal. As an image was being scanned by a camera, it was encoded, transmitted, decoded and scanned onto the display.
These line scanning techniques are tightly coupled with the characteristics of the CRT-based display technology available to the designers of television systems during the first half of this century. To produce an image, an electron beam is scanned across the inside face of a CRT covered with phosphors. In any one spot, the phosphors will illuminate, then decay, causing the light intensity to modulate or flicker. Thanks to an attribute of the human visual system called persistence of vision, we are able to integrate the information delivered by the scanning spot, creating the illusion of watching moving pictures.
There are many ways to scan a CRT display. Two methods have become commonplace: interlaced and progressive scanning. With interlaced scan, one half of the image--a video field--is reproduced by scanning all of the even lines in a frame, then the other field is reproduced by scanning all of the odd lines in a frame. With progressive scan, the first line of a frame is scanned across the top of the screen, then each successive line is scanned until the entire frame has been reproduced.
The use of interlace provided a well--balanced solution for the delivery of television images to early CRT displays. Some static resolution was sacrificed, compared to a progressive display with the same number of lines; however, the dynamic resolution was improved by delivering 50 or 60 pictures (fields) each second, versus 25 or 30. (Note that with the addition of color, the NTSC frame rate was modified to 29.97 frames/59.94 fields per second; for convenience, the 30 frame/60 field notation will be used throughout this book.)
Unfortunately, interlace imposes other compromises on image quality, compromises which have become evident as image acquisition and display technology have evolved up to, and beyond, the limits of the NTSC and PAL television standards.
With interlaced scanning, a video frame is acquired in two temporal sampling periods (each field making up the frame is captured at a slightly different moment in time); a frame therefore includes a mixture of spatial and temporal information. This makes it difficult to extract a temporally coherent still image from a video stream--this is why most video still stores allow the user to choose between a still frame and a still field. It also increases the complexity of temporal rate and spatial resolution transformations--for example, standards conversion between NTSC and PAL, and the image scaling and rotation techniques used in digital video effect systems. As we will see later in this chapter, the use of interlaced scanning also increases the complexity of the digital video compression techniques that form the basis for virtually all emerging digital television standards.
Interlace was an effective compression technique in an era dominated by analog technology and CRT displays. The use of interlaced scanning in new digital television systems has been highly contested, especially by the computer industry, which moved to the exclusive use of progressive scan display technology over the past decade. Whether the use of interlace will continue in new high resolution video formats remains to be seen. One thing is certain: broadcasters and videographers must deal with both forms of scanning during the migration to digital television.
Decoupling Digital Television Appliances From Its Analog Heritage
The emerging display technologies most likely to replace the CRTs in direct view and projection television displays have more in common with frame-based film projection than a line scanning system. Liquid crystal (LCD), plasma, and digital light processor (a.k.a. digital micromirror device) displays all have fixed sample sites that remain illuminated for essentially the entire field or frame duration. If two fields are combined to display a complete frame, the eye sees two temporal samples at the same time; this can cause severe image quality degradation. For proper display, the images must be de-interlaced, turning fields into frames by doubling the number of lines, approximating the missing information as close as possible. De-interlacing will also be required for progressively scanned CRT displays.
One of the major benefits from the move to digital television comes from the use of frame buffer memory in the receiver. The ability to buffer several video frames in memory is a critical requirement for the digital video compression techniques that will be used to squeeze high definition television into a 6 MHz (US) or 8 MHz (Europe) terrestrial broadcast channel.
Digital television receivers and set-top boxes designed to decode all of the ATSC (Advanced Television Systems Committee) Table 3 formats (see Glossary), will produce images at 480, 720 and 1080 lines. Both interlaced and progressive scanning techniques are used in the 480 and 1080 line format families (the 720 line format is progressive only). After decoding these images, they must be scaled for presentation at the resolution of the local display and, if necessary, de-interlaced.
In addition, DTV receivers will decode data and create raster images for display. These images may be displayed in lieu of video programs, in portions of the screen not occupied by the main program, or overlaid onto the video program(s).
Applications such as electronic program guides, news and weather services, sports scores, and closed captioning are examples of data broadcast services. Many proponents of data broadcasting hope to deliver new forms of content based on the technology and standards developed for the Internet and World Wide Web.
Digitizing The Image
The process of capturing images and converting them into bits involves two critical steps: sampling and quantization.
As the term implies, sampling is the periodic measurement of analog values to produce image samples. All film and electronic imaging systems utilize sampling to some extent.
The spatial resolution of film is limited by the density of grains of photosensitive dyes (image samples), while temporal resolution is limited by the frame rate and shutter angle (exposure time per frame period).
Analog video has always been sampled vertically because of the use of line scanning techniques. In a horizontal line scanning system, static and dynamic resolution are determined by several factors:
To digitize an image, we sample the analog video waveforms produced by a line scanning tube camera, or line and frame array image sensors.
Both line and frame array sensors sample images in three dimensions: horizontal, vertical and time. Line array sensors are used to scan still images, such as a film frame or the image on a photographic print or document.
With a tube-based image sensor, sampling takes place over the field or frame period, as the image accumulating on the sensor is scanned. The temporal skew from the first to the last sample in an interlaced video frame is 1/30th (NTSC) or 1/25th (PAL) of a second; samples on adjacent lines have a temporal skew of 1/60th or 1/50th of a second.
Modern CCD image sensors are frame-based capture devices. All of the sensor sites are capturing an image frame for the same portion of the temporal sampling period. Electronic shuttering is possible as the CCD sensor can dissipate charge (shutter closed) for a portion of the field or frame period, then accumulate charge (shutter open) to simulate the desired shutter speed.
The charges that accumulate during the frame sampling period are shifted to read-out registers. The CCD then produces an analog signal by scanning out the samples over time; this is analogous to the way a film frame is scanned.
A CCD can be designed to produce either an interlaced or a progressive scan output; some can output both. For a progressive scan output, every line is scanned. For an interlaced output, the charges on adjacent lines are summed to produce a video field. In the first field period, lines 1 and 2, 3 and 4, etc., are summed; in the second field period lines 2 and 3, 4 and 5, etc., are summed to provide the one line offset between fields.
Interlaced analog signals can be digitized with excellent results, as we have seen with the ITU-R 601 digital component sampling standard. Analog and digital component processing are now used as intermediate steps in the process of creating high quality analog NTSC and PAL signals, and digitally encoded MPEG-2 bit streams.
The static and dynamic resolution of a digitized image stream is directly related to the sampling frequency and the level of quantization applied to each sample.
Quantization
If we are capturing a document with black text on a white background, it is sufficient to represent the samples with a single bit: if the bit is set to 0 we have white, if it is set to 1 we have black. If we wish to capture an image with intermediate values, for example a gray scale that changes from white to black, we will need many values or quantization steps to represent each sample. With 8-bit quantization, we can represent 256 levels of gray; 10-bits provide 1,024 discrete quantization steps.
The number of quantization levels determines the accuracy with which a sample can be represented. More quantization steps provide greater accuracy and the ability to reproduce the small levels of difference between samples in smooth gradients (see figure 8: Quantization Levels).
Sampling is, at best, an approximation of the analog world. The actual level being sampled may differ from the sample value for a number of reasons. Even if the sampling system were perfectly accurate, a quantization error of one-half step is still possible. Sampling systems are rarely that accurate; in the real world, an error of a full quantization step is quite probable. To improve sampling accuracy we can oversample the image, then resample to the sample grid we will use for distribution.
The bit that determines the choice between two adjacent quantization levels is called the least significant bit. It is difficult for the human visual system to detect single-step quantization errors in systems with good dynamic range (typically eight or more bits per sample). Thus in uncompressed systems, the least significant bit can be used to encode additional information without significantly impacting image quality.
In addition to errors introduced during sampling, subsequent image processing and encoding can introduce the following quantization errors:
As we will see later in this chapter, selectively quantizing certain information within an image forms the basis for many of the video compression techniques used in digital television.
 |
| How much dynamic range does a television system need? In order to see what's going on in the shadows, or details in picture highlights, we need many picture levels to show small differences. In the image above, each sample is stored as a 5-bit value; this allows 32 levels of quantization between white and black (notice the vertical "bars"). In the image below, each sample is stored as an 8-bit value--256 levels of quantization between white and black. |
 |
| Using 8-bit samples, ITU-R 601 places black at value 16 and white at value 235. This permits values below black and above white; these values do not exist in RGB signal representations that place black at value 0 and white at value 255. ITU-R 601 also permits luminance sampling with 10-bit values (1,024 levels); this improves dynamic range and conversions to 8-bit RGB values for processing and display. In 10-bit, black is at value 64 and white is at value 940. |
The sampling frequency establishes limits on the spatial and temporal frequencies that an imaging system can reproduce without the introduction of perceptible aliasing artifacts. In terms of spatial resolution, sampling theory indicates that the highest spatial frequency we can reproduce--without aliasing--will be slightly less than one-half the sampling frequency.
Let's use the ITU-R 601 component digital sampling specifications as an example. This specification is based on multiples of a 3.375 MHz sampling rate, a number carefully chosen because of its relationship to both NTSC and PAL. Two levels of quantization are permitted for the luminance component: 8- and 10-bit. The color difference components are quantized at 8-bit.
The sampling frequency for the luminance (Y) component of the signal is 13.5 MHz. Thus, the upper limit on the spatial frequencies that can be represented will be slightly less than 6.75 MHz. This is sufficient for the 6.0 MHz luminance bandpass of PAL, and represents significant horizontal oversampling relative to the 4.2 MHz luminance bandpass for NTSC.
The sampling frequency for the color difference components, R-Y and B-Y, is 6.75 MHz. Thus the upper limit on the spatial frequencies that can be represented will be slightly less than 3.375 MHz. This is significantly higher than the 1.5 MHz bandpass for the color components in both PAL and NTSC. This additional color resolution is quite useful in the generation of color mattes, providing yet another reason to use component rather than composite video signals in the video composition process.
A notation system has been adopted to describe the relative sampling frequencies for the luminance and color difference components of the digital video signal; this notation is referenced to the 3.375 MHz basis for the ITU-R 601 standard. The luminance sampling frequency is four times the base frequency; the color difference sampling frequency is two times the base frequency. Thus this sampling relationship is know as 4:2:2, representing luminance and each color difference component. These sampling parameters are used in the D1, D5, D9, Digital Betacam and DVCPRO50 tape formats.
The notation 4:4:4 indicates that each of the signal components is sampled at 13.5 MHz. This corresponds to the signals produced by the individual image sensors, thus the 4:4:4 notation is often used for either YUV or RGB components.
The notation 4:1:1 indicates that the color difference components have one-quarter the resolution of the luminance signal; this correlates well with luminance and color resolution delivered by NTSC and PAL. 4:1:1 sampling is used in the consumer DV format and the 25 megabit per second (Mbps) versions of DVCPRO and DVCAM.
In the production environment, it is often useful to store a matte channel that can be used to overlay portions of an image in a video composition. The matte can be based on color information in the original image (a chromakey), luminance information in the original image (a luminance key) or a linear control signal (an alpha channel or linear key).
Linear key and alpha channel signals typically have the same sample structure as the luminance or Y channel portion of the signal; however, the number of quantization levels may be reduced. The value of an alpha channel sample is used to establish the level of blending or transparency for the image samples (Y, R-Y, B-Y) in the same spatial location. The number of quantization levels in the alpha channel determines the number of levels of transparency available; to reproduce smooth gradients, such as shadows, it is typical to represent alpha channels with 8-bit values (256 levels of transparency). The standard notation for an alpha channel is to append it to the image sampling notation: 4:4:4:4 and 4:2:2:4 indicate images with full resolution alpha channels.
As all of the sample representations described to this point are based on interlaced scanning, it is important to note that the color sub-sampling affects only horizontal resolution. All of these systems sample luminance and both color difference components on every line.
As we learned earlier, the underlying rationale for color sub-sampling is based in the limits of human visual perception. These limits exist for both horizontal and vertical resolution, although research indicates that the visual system is forgiving of inequalities in H and V resolution in the range of 2:1 to 1:2.
One of the major reasons that today's interlaced video systems do not attempt to limit the vertical color resolution is the mixing of spatial and temporal information between the fields that make up a frame. It is nearly impossible to accurately separate the temporal and spatial information, and to predict the information that was not sampled in the first place. Proper sub-sampling of vertical color resolution involves the same complexity, and inherent limitations, found in devices used for temporal and spatial resampling, including standards converters, digital video effect systems and display processors that de-interlace and double or quadruple the number of lines.
By comparison, with film and progressive scan image acquisition, it is relatively easy to sub-sample vertical color resolution, thereby eliminating more information that the human visual system does not process.
Unfortunately, this creates a rather nasty problem with the notation system used to describe color sub-sampling. What is the accepted notation for a system that reduces both horizontal and vertical color resolution by one-half?
4:2:2 is probably the most accurate description, but it's already taken. For reasons that are not obvious, the notation used for this form of color subsampling is 4:2:0. This is the designated sampling structure for the MPEG-2 video compression that will be used for digital television broadcasts.
Before we leave the subject of image sampling, a brief discussion about the advantages of oversampling are in order. In his book, The Art of Digital Video (1990, Focal Press) John Watkinson makes the point that television systems have evolved from times when many of the freedoms of modern image acquisition and display technology were not available.
"The terrestrial broadcast standards of today were designed to transmit a signal which could be fed to a CRT with the minimum processing. The number of lines in the camera, the number of lines in the broadcast standard and the number of lines in the display were all the same for reasons of simplicity, and performance fell short of that permitted by sampling theory. This need no longer be the case. Oversampling is a technique which allows sampled systems to approach theoretical performance limits more closely. It has become virtually universal in digital audio, since at the relatively low frequencies of audio it is easy to implement. It is only a mater of time before oversampling becomes common in video."
While less efficient from the viewpoint of bandwidth requirements, oversampling has much to offer in terms of high quality image acquisition and subsequent processing. The video industry is unique in that the same sampling grid is typically used for image acquisition, processing, transmission, and display. To prevent aliasing, an optical low pass filter is generally placed between the lens and image sensor(s), limiting the spatial frequencies present to less than half of the sampling frequency. To properly reconstruct the image, a similar low pass filter should be placed in front of the display to eliminate the aliasing artifacts it may produce. Unfortunately, viewers might object if manufacturers placed such a filter over the display, so we live with these aliasing artifacts.
It is not likely that viewers will purchase separate displays for each of the formats in the ATSC digital television standard, or that manufacturers will offer low-cost displays that synchronize to each of the 36 formats defined by the standard. Even if the display could operate in more than one format, the problem of combining images from multiple sources--to support picture-in-picture, for example--would still exist.
Therefore, it is likely that the display component of a digital television system will operate with image refresh parameters that provide optimal image quality for that display, and that all of the transmission formats will be re-sampled in the receiver to match those parameters. This will require de-interlacing and other forms of image processing in the receiver.
Bottom line: The best way to assure that high quality images are presented on screens that come in many sizes and resolutions is to encode only the highest quality images for transmission. This does not necessarily mean the highest resolution images, although oversampling, relative to the resolution eventually encoded for distribution, will pay many dividends in the emerging digital world.
An Introduction To Digital Video Coding
We are now prepared to begin the discussion of digital video encoding techniques, otherwise known as digital video compression or bit rate reduction.
Digital video encoding is based on a toolbox approach to the problem. A variety of coding techniques are available from the toolbox; appropriate tools can be selected and employed to match application and bandwidth requirements. These digital video coding tools can be divided into several broad categories:
Lossless: Ensures that the original data is exactly recoverable.
Lossy: The original data is not completely recoverable. Coding is based on the theory that small quantization errors in the high-frequency components of the image are not perceptible by the human visual system.
We can further divide digital video coding into spatial and temporal coding techniques: Self-referential or Intra-frame: Bit rate reduction is based entirely on redundancy within the image that is being coded.
Predictive or Inter-frame: Bit rate reduction is based on the redundancy of information in a group of pictures (a small number of consecutive video frames). Motion compensated prediction is typically used, based on reference frames in the past and the future. Redundant information is removed by coding the differences between a prediction of the image data within a frame and the actual image data.
Lossless coding techniques have an obvious advantage, in that the original sample data can be recovered without the introduction of quantization errors. Unfortunately, these techniques do not provide enough compression efficiency to meet the bandwidth constraints further down the digital video food chain.
There are several lossless coding techniques employed in digital video compression systems. The first is run length encoding (RLE). This technique counts the number of samples along a line with the same value; this value and the number of samples--the run length--are stored, followed by the next run, etc. The efficiency of this technique is scene-dependent. A smooth gradient in the vertical direction encodes very efficiently, as every sample along a line is the same. A smooth gradient in any other direction does not compress at all, as every sample on every line is different. One of the goals of the compression techniques we are about to examine is to increase the runs of identical pixel values to improve the efficiency of this lossless encoding technique.
Reversible transforms are employed in virtually all image coding techniques in common use today. In essence, the sample data is transformed into a different representation that has advantages in terms of compression efficiency. If the transformed data is not modified, the transform can be reversed, recovering the original data.
Entropy coding is, from a historical perspective, one of the oldest data compression techniques. The Morse Code for telegraphy is an example of an entropy code. The most common letter (in English) is E so it gets the shortest code (one short tone--a dot). Q is much less common, so it is assigned a long code (two long tones, one short tone, one long tone--dash-dash-dot-dash). This speeds up transmission on average.
Lossy coding techniques throw information away. Typically, the sample data is subjected to a reversible transform; the transformed data is then quantized to eliminate small differences, then run length and entropy coded. When the process is reversed, the sample data is reconstructed, hopefully with only minimal degradation.
Intra--frame Video Coding
The discrete cosine transform (DCT) is currently the most widely used transform for video compression. The wavelet transform has also enjoyed popularity for intraframe video coding; however, it does not lend itself as well to the inter--frame compression techniques that provide much of the efficiency in MPEG video compression. The DCT is the basis for the intra--frame coding techniques used in JPEG, Motion-JPEG and MPEG, as well as many video recording formats including, D9 Digital Betacam, DV, DVCAM and DVCPRO.
MPEG is the acronym for the Moving Picture Experts Group, which creates standards under the auspices of the International Telecommunications Union and ISO (International Standards Organization). This standards group has close ties with JPEG--the Joint Photographic Experts Group--which develops standards for the compression of still images.
As video is nothing more than a succession of still images, a variation called Motion-JPEG or M-JPEG is used for intraframe video compression. Because of low cost implementations and the need to access each frame easily for frame-accurate edits, M-JPEG is currently the compression codec of choice for the majority of nonlinear video editing systems.
The DCT is a reversible transform that converts sample data from spatial order into frequency order; if the resulting coefficients are not quantized, the process can be inverted, returning the original data set. If coefficients have been quantized, they can still be passed through the transform multiple times without further loss; this attribute is very important, as with reasonable care, it enables images to pass through multiple DCT-based compression codecs without additional degradation.
The DCT is applied to small eight-by-eight sample regions of the luminance and color difference components that make up an image. By breaking the image up into small blocks, the effect of the transform is localized. The block structure also plays an important role in the motion-compensated prediction techniques used for interframe coding.
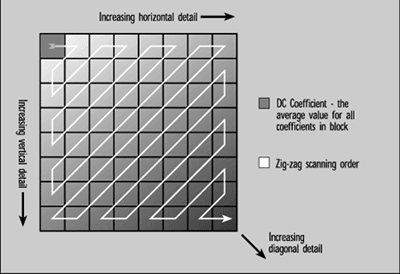
figure 9. Ordering of DCT coefficients.
When the DCT is applied, sample data is transformed from the spatial domain--the horizontal and vertical locations of the pixels--into the frequency domain. The resulting DCT coefficients are arranged on the basis of the spectral content of the samples. In figure 9: Ordering of DCT Coefficients, we see how the sample information has been reordered in the frequency domain. The upper left corner of the eight-by-eight matrix of transform coefficients contains the DC coefficient; this is the average value for the entire block. This is the only coefficient required to represent a solid block of luminance or color information.
Moving away from the DC coefficient to the right, we find coefficients that differ from the DC coefficient based on increasing horizontal frequency content. Moving down, we find increasing vertical frequency content. Large differences typically indicate the presence of high frequency edge information within a block. Small differences typically indicate gradual changes, such as the subtle shifts in luminance or color in the sky. As you will see, small differences are actually more difficult to deal with than large ones.
Since image information is localized with the DCT blocks, it tends to be highly correlated. The transform will typically produce a limited number of spectral coefficients, leaving many holes in the data (coefficients with a value of "0"). These holes are eliminated using run length coding--coefficients are read out in zigzag order to maximize the run lengths of "0" coefficients.
Huffman (entropy) coding of the coefficients is used for additional data reduction. Lower frequency coefficients, which tend to occur frequently, are given short codes; higher frequency coefficients, which occur less frequently, are given longer codes.
The DCT transform and entropy coding do not cause any loss of picture information. As information content typically changes from scene to scene, the amount of data produced by the DCT for each frame varies with scene content. Unfortunately, for the most demanding video images, the DCT yields, on average, a 2:1 compression ratio. Many nonlinear editing systems now handle the bandwidth peaks required for 2:1 compression, and thus can support the lossless mode available in M-JPEG codecs.
To achieve higher levels of compression, it is necessary to quantize the DCT coefficients in a nonlinear fashion. This is where the DCT has major advantages over NTSC's analog compression techniques, and where the MPEG, M-JPEG and DV family tree begins to branch.
NTSC uses filtering techniques to limit the maximum frequency of the luminance and color components of the signal--without regard to the total amount of information in the image. Based on the spectral content of video images, we find that significant portions of the NTSC signal contain little or no information. Add to this the portions of the signal that contain synchronizing information for the CRT display, and we see that there is plenty of room left in which to squeeze more information about the images, including high frequency details that are removed by the bandpass filters.
With the DCT, it is possible to quantize coefficients on a selective basis; high frequency detail can be preserved for most scenes. The quality of the resulting images depends on two factors: the total information content in the image and the target bit rate. If the level of quantization is held constant, the bit rate of the compressed image stream will vary based on the information content. If the bit rate is held constant, the level of quantization must vary to compensate for changes in the information content of the images.
Quantization of DCT coefficients is accomplished by dividing the coefficients by values contained in a quantization or Q-Table. Dividing by 1 leaves a coefficient unchanged; dividing by larger numbers reduces the differences between coefficients. This reduces the number of different coefficients, and thus improves compression efficiency.
Q-tables can be tuned to achieve specific compression levels, or for specific kind of image information. JPEG and M-JPEG use the same Q-table for all of the DCT blocks (usually 8x8 pixels) in an image. Thus like NTSC, the table filters every block the same. DV and MPEG allow the Q-table to be adjusted for each macroblock in the image--a macroblock is small group of DCT blocks, typically four blocks or 16x16 pixels. Based on image statistics derived by passing the image through the DCT transform, the level of quantization can be adjusted for each macroblock, allocating more bits to the most demanding regions of the image.
The highly selective quantization process puts the coded bits into the frequencies to which our visual system is most sensitive, while limiting the bits that code the higher frequencies to which we are less sensitive. Used in moderation, the quantization of DCT coefficients is a highly effective compression technique.
The presence of high frequency transitions within a DCT coding block--such as those that occur in text and graphics--influences all of the coefficients within that block. To properly decompress the image without artifacts, each coefficient must be restored to its original value. If many coefficients are modified in the quantization process, the result will be the periodic disturbance of the pixels around the high frequency transition. This is referred to as quantization noise.
High quality analog or digital component video, sampled at rates comparable with ITU-R 601, can typically be encoded with compression ratios in the range of 2:1 to 5:1, with no visible loss in image quality. As the level of quantization increases, we begin to see noise around high frequency edges.
Another defect of the quantization process, which is often more noticeable than the high frequency quantization noise, occurs when there are subtle changes within a region of the image, for example in the sky, or in smooth gradients. Higher levels of quantization will eliminate the small differences, causing the entire block to become a solid rather than a gradient. As a result, the region will take on a quilted appearance. If we quantize at even higher levels, the entire image will break down into blocking artifacts, resembling pixelation.
If we quantize the DCT too coarsely, the end result is the generation of quantization noise. It is somewhat ironic that noise is the most significant barrier to high quality, DCT-based compression. Noise appears as very high frequency information, with no correlation to the samples that are being encoded. When the DCT is presented with a noisy signal, compression efficiency can be severely impacted.
This is one of the principal reasons that new digital video acquisition formats digitize and compress image samples before they are recorded. When applied properly, intraframe digital compression techniques can be used to preserve the highest levels of image quality.
Inter--frame Video Coding
When the DCT is used in conjunction with prediction-based inter--frame video coding techniques, we enter the sometimes bizarre world of MPEG. Unlike intra--frame techniques, which require approximately the same performance for encoding and decoding, the MPEG encoding/decoding process is highly asymmetrical. Significantly greater processing power is required to encode an MPEG data stream than to decode it.
MPEG-1 and MPEG-2 were developed to encode moving pictures at a variety of bit rates--from what some consider near-VHS quality at 1.5 Mbps to near-HDTV quality at 15 to 30 Mbps. MPEG-1 is optimized for the coding of video frames at low bit rates (1 to 3 Mbps); MPEG-2 is optimized for the coding of video fields or frames at higher bit rates (3 to 10 Mbps for SDTV, 15 to 30 Mbps for HDTV).
Intra-- and inter--frame video coding tools, along with audio encoding techniques and a data transport protocol, are part of what has become known as the MPEG-2 toolbox. Specific combinations of tools, optimized for various performance and application requirements, are known as profiles. For example, MPEG-2 Main Profile at Main Level (MP@ML) supports sample rates--for the active area of the video image--of up to 10.4 samples per second; MP@ML is optimized to handle existing digital video formats based on the ITU-R 601 sampling specifications. The difference in sample rates, 10.4 million versus 13.5 million, relates to the time spent sampling the video blanking intervals.
In order to achieve the higher levels of compression required to squeeze HDTV into a 6 to 8 MHz channel, we need to eliminate temporal redundancy. The interframe or temporal coding tools used by MPEG are based on a technique called Differential Pulse-Code Modulation (DPCM). The DPCM coding loop lies at the heart of MPEG coding techniques.
Differential PCM comes out of the intuitive concept that sending the difference between two things takes less information, or bandwidth, than sending the two things themselves. For example, if a television picture is stationary, why should we send the same picture over and over again, 60 times a second? Why not just send the difference between successive pictures?
If we can predict, with reasonable accuracy, what a frame will look like, the differences will be significantly smaller than the frames themselves--for still images the differences will consist primarily of noise or film grain. This provides a significant boost in compression efficiency when compared with intraframe compression techniques.
MPEG specifies three types of "pictures" that can be coded into a data stream:
Intra-coded picture (I): The original image is encoded using information only from itself. DCT compression techniques are used to code the image frame, or two interlaced fields. I pictures provide access points to the data stream.
Predictive-coded picture (P): A picture coded using motion-compensated prediction from a past reference picture. The difference between the actual image and the predicted image is encoded using DCT compression techniques.
Bidirectionally-predictive coded picture (B): A picture coded using motion-compensated prediction from past and future reference pictures. The difference between the actual image and the predicted image is encoded using DCT compression techniques--it is not an average of the previous and future frame. B pictures provide the most efficient coding, however, a third memory buffer is required in addition to the buffers for past and future reference (I and P) pictures. Fast search modes are facilitated by ignoring B pictures.
MPEG streams can be coded using I frames only, I and P frames, I and B frames or I, P and B frames. The coding of I frames only is, in fact, virtually identical to the intraframe coding techniques discussed in the previous section.
MPEG profiles for program distribution utilize 4:2:0 sampling, IP or IPB frames, and the bit rate constraints described at the beginning of this section. The MPEG-2 Studio Profile was created for production and contribution quality video encoding. This profile permits the use of 4:2:2 sampling, any combination of I, P and B frames, and bit rates of up to 50 Mbps. For example, the Sony Betacam SX format employs 4:2:2 sampling, I and B frames, and a bit rate of 18 Mbps.
The syntax of MPEG data streams is arranged in a layered hierarchy. Starting at the bottom of the hierarchy and working up:
Block: An eight-row by eight-column orthogonal block of pixels. This is the basic unit to which the discrete cosine transform is applied.
Macroblock: In the typical 4:2:0 picture representation used by MPEG-2, a macroblock consists of four 8x8 blocks of luminance data (arranged in a 16x16 sample array) and two 8x8 blocks of color difference data which correspond to the area covered by the 16x16 section luminance component of the picture (see
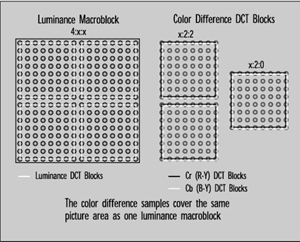
The macroblock is the basic unit used for motion compensated prediction.
Slice: A series of macroblocks. A slice is the basic synchronizing unit for reconstruction of the image data and typically consists of all the blocks in one horizontal picture interval--typically 16 lines of the picture.
Picture: A source image or reconstructed data for a single frame or two interlaced fields. A picture consists of three rectangular matrices of eight-bit numbers representing the luminance and two color difference signals.
Group of pictures (GoP): A self-contained sequence of pictures that starts with an I frame and contains a variable number of P and B frames.
The MPEG coding loop requires one or two frames of the video stream to be stored in memory, providing the reference image(s) for motion compensated prediction. Predicted frames require a second or third memory buffer.
A significant amount of the computational work in MPEG involves motion estimation--searching for matching macroblocks in two frames, to determine the direction and distance a macroblock has moved between frames (motion vectors).
Decoders use these motion vectors to reposition macroblocks from the reference frames, assembling them in a memory buffer to produce the predicted image. The encoder also contains a decoder, which is used to produce the predicted image; this prediction is subtracted from the original uncompressed frame, hopefully leaving only small differences. These differences are encoded using the same DCT-based techniques used to encode I frames.
The MPEG coding loop is more efficient when it can see what things look like in the future. When we start coding a new picture sequence with an I frame, moving objects obscure the background behind them; there is no way to predict what those background pixels will look like until they are revealed. If we skip forward a few frames, and we can learn two very important things: 1) what the pixels that are revealed look like; 2) the motion vectors for the objects that moved.
An MPEG encoder must have multiple frame buffers to allow it to change the order in which the pictures are coded. This is known as the coding order. With one frame of buffer memory forward predictions can be used to create the next P frame. With two frames of buffer memory bi-directional predictions can be used to create one or more B frames between the reference I and P frames.
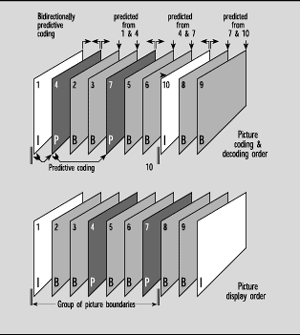
An encoder that works at less-than-realtime rates has no problem in cheating time. It just fills its buffers with a bunch of pictures, then codes them out of order. In order to peek into the future, a realtime MPEG encoder must introduce a period of latency between the actual time of an event and the time you see it--the latency is equal to the number of frames of delay built into the encoder (this will make off-air monitoring during live news remotes almost impossible).
If a non-realtime encoder runs into a tough coding sequence, it can slow down and do a better job of motion estimation. But a realtime MPEG encoder has a finite amount of time to make encoding decisions and thus may make some compromises--either more picture artifacts or a higher data rate for the same picture quality.
A group of pictures (GoP) begins with an I frame. A GoP can be a single I frame, or it may include a variable number of P and/or B frames. GoP lengths typically increase with the frame rate of the source material, and they tend to be longer with progressive scan source material.
A new GoP begins with the next I frame: this frame may be unrelated to the previous GoP--e.g., when there is a scene cut--or it may be a continuation of the previous GoP. Because images are coded out of order, B frames that are predicted from an I frame in the following GoP are included in that GoP (see figure 11: The MPEG Coding Loop).
When a GoP contains P and B frames and after the I frame is coded, we skip ahead a few frames and code a P frame. A forward prediction is created, based on the I frame. With I and P frames in the buffers we can now make accurate predictions about the B frames that are in-between. Again, we predict what these frames should look like, then encode the differences from the actual image.
An MPEG decoder uses the reference I and P picture data and motion vectors to re-construct the B pictures. The difference information is then added to the predictions to reconstruct the images that will be displayed.
All of the serialized processes that are required for an MPEG encoder can be run on general-purpose computational engines. In most cases these software encoders are allowed to take as much time as they need to obtain maximum image quality.
Realtime encoders may take advantage of the slice level of the MPEG syntax to divide the image into sections that can be encoded in parallel. Each slice of the image is encoded using a separate processor, and several additional processors are used to keep track of information that is moving between slices. Early realtime MP@ML encoders used as many as 14 parallel processors to encode the image.
The coding of interlaced images requires an additional layer of sophistication, due to the temporal skewing between the fields that make up each frame. When the fields are combined, the skewing between samples interferes with the normal correlation between samples--the skewing looks like high frequency edge information.
M-JPEG systems avoid this problem by coding individual video fields; they treat the interlaced video information as if it were 50 or 60 video frames with half the number of lines. While MPEG could use the same approach, there are more efficient ways to deal with interlace; MPEG-2 added several techniques to deal with the coding of interlaced video images.
The first is adaptive field/frame-based coding at the macroblock level. An MPEG macroblock contains four DCT coding blocks. When significant skewing is detected within the DCT blocks, the samples from one field are moved into the two upper blocks while the samples from the other field are moved into the lower blocks. This improves the correlation of image data, significantly improving the coding efficiency of each DCT block (see figure 12: Field/Frame DCT Coding).
The combination of quantization at the macroblock level and field/frame based macroblock coding, on average, allows intraframe MPEG-2 coding a 2:1 improvement in compression efficiency over M-JPEG. This may eventually lead to the use of I frame MPEG-2 coding in video editing applications as the cost of MPEG encoders decline.
The second technique, added in MPEG-2 to deal with interlace is adaptive field/frame-based motion prediction. This complements the use of adaptive field/frame-based block coding, allowing separate motion vectors to be generated for the blocks that make up each field.
The MPEG specification does not define how encoding decisions are to be made. It only specifies what an MPEG-compliant bit stream must look like. Thus, it is up to the manufacturers of encoders to differentiate themselves in the marketplace based on major feature/benefit criteria: price; realtime versus non-realtime operation; and picture quality versus bit stream data rate.
|
This figure illustrates the field/frame based DCT coding techniques employed in MPEG-2 for the coding of interlaced frames. The images in this diagram were captured off of a cable television feed and have been enlarged to show their sampling structure. Because of horizontal motion between fields periods, there is significant skewing in the samples. By reordering the samples within a macroblock, it is possible to improve coding efficiency.
|
 |
By eliminating the redundancy in portions of the image that are stationary, more bits can be used to reduce the quantization of DCT coefficients. Thus MPEG compression can typically operate with compression ratios in the range of 10:1 to 50:1.
The downside to the use of MPEG compression at highly constrained bit rates is that image quality may vary with scene content. When there is little motion, more high frequency coefficients are preserved and the image will be sharper. Scenes with rapid motion and lots of image detail--for example a pan from one end of the court to the other during transitions in a basketball game--may stress the encoder. This may result in the loss of resolution and increased quantization noise, or in the worst case, blocking artifacts. Fortunately, as long as the level of artifacts is not too severe, these fluctuations in image quality correlate well with the static and dynamic resolution capabilities of the human visual system.
MPEG also has problems dealing with certain common video production effects, notably the dissolve and fade-to-black. During these effects, every sample is changing with each new field or frame; there is little redundancy to eliminate. The cross dissolve is further complicated by the co-location of two images with objects moving in different directions.
Work is already underway on MPEG-4, which will deal with more advanced techniques to encode multiple image objects for transmission and compose these objects locally for display.
What About Audio Coding?
Unlike video, audio is a continuous signal. There is no frame rate, no temporal redundancy to eliminate except when things go silent. Like video, the spectral content of audio varies over time, and with it, the information content of the signal at any moment. As with the video compression techniques described previously, the goal of the Dolby Digital/AC-3 compression algorithm, chosen by the ATSC for audio coding, is to pack information into the transmission channel more efficiently.
The Dolby Digital/AC-3 compression algorithm can encode from 1 to 5.1 channels of source audio from a PCM (Pulse-Code Modulation) representation into a serial bit stream at data rates ranging from 32 kbps to 640 kbps. The 0.1 channel refers to a fractional bandwidth channel intended to convey only low frequency (subwoofer) signals. Four channels provide surround sound and the fifth center channel delivers dialog.
The audio encoders are responsible for generating the audio elementary streams which are encoded representations of the baseband audio input signals. The flexibility of the transport system allows multiple audio elementary streams to be delivered to the receiver. These streams can include complete audio programs or a separate audio program for music and natural sound that can be mixed with dialog in multiple languages, enhanced audio for the hearing impaired, program related commentary and emergency audio messaging.
At the receiver, the transport subsystem is responsible for selecting which audio streams to deliver to the audio subsystem. The audio subsystem is responsible for decoding the audio elementary streams back into baseband audio.
The Dolby Digital/AC-3 algorithm achieves high compression efficiency by coarsely quantizing a frequency domain representation of the audio signal. For example, an uncompressed 5 Mbps audio program with 5.1 channels will typically be compressed to 384 Kbps--a 13:1 compression ratio.
The audio compression system consists of three basic operations. In the first stage, the representation of the audio signal is changed from the time domain to the frequency domain. As with video, this is a more efficient domain in which to perform psychoacoustically based audio compression.
The resulting frequency domain coefficients are then encoded. The frequency domain coefficients may be coarsely quantized, because the resulting quantizing noise will be at the same frequency as the audio signal, and relatively low signal-to-noise ratios are acceptable due to the phenomenon of psychoacoustic masking. The bit allocation operation determines, based on a psychoacoustic model of human hearing, the actual SNR (signal-to-noise ratio) that is acceptable for each individual frequency coefficient. The frequency coefficients can then be quantized to the necessary precision to deliver the desired SNR and formatted into the audio elementary stream.
The Dolby Digital/AC-3 encoding system chosen for the ATSC standard is one of several alternatives for the delivery of enhanced audio service and surround sound, that will coexist in the emerging world of digital television. The MPEG-2 standard includes tools for the coding of a variety of audio formats. MPEG-2 audio is used on DVD (as is Dolby Digital/AC-3), and may be used in some areas of the world for terrestrial broadcasts.
Like Dolby Digital/AC-3, the MPEG-2 audio tools permit the coding of multi-channel audio. The basic stereo mix is encoded to be compatible with the MPEG-1 audio standard. Support is provided for a variety of multi-channel and surround systems including Dolby Pro Logic. These modes include: three channel, with a center dialog channel; four channel, with a center channel and single surround channel for rear speakers; 5.1 channels with center channel, separate right and left surround channels and subwoofer channel; and 7.1 channels, like 5.1 with the addition of right and left center channels for better dialog placement.
Dealing With Digital Compression In The Broadcast Facility
We have completed a behind-the-curtain peek at the video compression techniques that made analog television possible, and the digital techniques that will enable the next generation of digital television broadcasting. We are now entering a transition period where we must deal with both, and begin the process of upgrading broadcast facilities to take full advantage of the new services enabled by digital broadcasting.
One area of concern during this transition period relates to the proper handling of analog and digital video signals in the broadcast facilities: Where and how to use various compression techniques appropriately to maximize the quality ultimately delivered to the viewer, and what to avoid to prevent unnecessary degradation of signal quality.
Perhaps the best way to look at this issue is to consider the use of appropriate video compression techniques as we move from image acquisition, through the production and distribution environments, and finally encode content for digital transmission--the digital video food chain.
From this perspective, the content creation and distribution process looks something like a bandwidth funnel; at certain points along the food chain, we must throw information away to meet bandwidth constraints as we move from acquisition to final program distribution.
As is the case with current digital component systems, the first steps in bit rate reduction will take place during image acquisition. For many applications, it may be desirable to preserve virtually all of the image content within each frame to facilitate subsequent image processing. At this end of the video food chain, we can generally afford more storage bandwidth, thus we can preserve more of the original image information.
The next major squeeze typically takes place when content is encoded for distribution--perhaps through a satellite link--to facilities where it may be subject to further modification. This is often referred to as contribution quality. Modifications may include editing and integration with other content; thus, the bit rate reduction techniques used for contribution quality typically reflect these requirements.
Finally, when the content is ready for broadcast, we can take the last step in bit rate reduction. We squeeze what's left into the constrained bandwidth of a digital broadcast channel, or squeeze further to deliver a multiplex of programs and data broadcasts. An HDTV program, originally acquired at a bit rate of 1.2 gigabits per second (Gbps) is compressed by a factor of 66:1 to fit in an 18 Mbps portion of the 19.39 Mbps digital channel. SDTV programs sampled using ITU-R 601 specs will typically be compressed by factors of 20 to 40:1 to produce bit streams in the range of 4 to 8 Mbps.
Unlike the analog television food chain, if we preserve the data--both images and metadata--we can maintain quality as content moves from one process to the next.
What is metadata? It is data about the data. This can include ancillary data such as time code, or text-based descriptors of the content. It may also include information about the image processing history, links to the original source and related versions, and encoding decisions that were made the last time the images or sound were encoded. Things like the choice of quantization tables for each DCT coding block, and motion vectors.
If we maintain the metadata about the processing history of the content, we can use it to save time and preserve quality when the content is re-encoded. It is only when we modify the data, or throw more data away that the potential for errors exists. The term used to describe these losses is concatenation errors.
For example, it may be necessary to convert the representation of an image stream (file format and encoding techniques) when it is transferred from a field acquisition format to a nonlinear editing system. If we are working the same sampling parameters, and both systems use block based DCT coding, it should be possible to effect this transfer with no loss in quality, assuming that the target system does not impose additional bandwidth constraints that require additional quantization of the DCT coefficients.
In order to facilitate this type of file conversion, the bit stream must be decoded to the DCT coefficient level, reversing the entropy coding, quantization and field/frame based ordering of the coefficients. The coefficients can then be re-encoded using the same quantization decisions used when the content was originally encoded.
If the conversion involves moving from an environment with different levels of quantization for each macroblock, to a single level of quantization for each block in the image, we can still preserve all of the DCT coefficients by choosing the table with the lowest level of quantization (highest quality).
A related approach to the minimization of concatenation errors with MPEG-2 compression has been developed by a European research consortium called the Atlantic Project. These European broadcasters are trying to deal with the problems of adding information to programs as they move from the network, through regional operations centers, and finally to local transmission facilities.
The Atlantic decoding/re-encoding process uses a technique called Mole Technology. When an MPEG-2 stream is decoded, the metadata about the encoding decisions is buried in "uncompressed 601" signal; this is accomplished by using the least significant bit of each sample to encode the Mole data. If the content is not modified, the Atlantic encoder recognizes the presence of the Mole, and uses the encoded data to exactly reproduce the original encoding decisions. If the mole is disturbed, then the frame or a section of the frame must be re-encoded, with the potential for concatenation errors.
Another approach is to pass MPEG-2 encoded streams through, without modification, and add ancillary data, which can be turned into an image object and composed with the MPEG-2 video in the receiver. This approach would require receiver standards that are currently being developed, but may not be deployed in early digital television appliances. The MPEG committee is currently working on the MPEG-4 standard, which provides a syntax for the composition of a video background with multiple video foreground objects and locally generated graphics.
Like HTML, an object oriented method for composing visual information in a remote viewing environment, the MPEG-4 concepts will allow future DTV devices to compose video information in unique ways for local consumption. This is analogous, in many ways, to moving the "master control switcher" into the DTV receiver. Rather than splicing all content into a single program stream for decoding, the receiver will have the ability to switch between sub-streams, e.g., with localized versions of commercials, and to overlay visual objects, such as commercial tags, localized to the receiving site. Transitions such as dissolves and fades can be applied in the receiver, after decoding of the image streams.
At the beginning of this section, I suggested that it would be appropriate to let go of preconceptions founded in analog thinking. Concatenation errors are one of those problems that looks troubling, from an analog perspective, yet may be almost irrelevant in the world of digital television broadcasting.
Out of necessity, analog production techniques evolved as a serialized process. The first generation of digital tape formats and production equipment made it possible to eliminate the quality losses associated with multiple generations of image processing. The first generation of digital nonlinear editing and image composition products turned editing and image composition into a parallel processing task.
Nonlinear systems work with the original bits, acquired with digital formats, or first generation digitized copies. Any composition of any complexity can be created in one additional generation, by decoding each object layer to the original samples, combining all the objects, then compressing the result. The process is non--destructive of the original source. A different version is just a different playback list.
Furthermore, many of these tools are resolution independent. They can be configured to output any format at any resolution, and accept visual objects from many sources, using many encoding formats, at many resolutions.
What other approach could possibly work for a digital broadcast standard with 36 optional video formats? From this perspective, it quickly becomes apparent that formats are an artifact of the analog world. Now there is only data.
[an error occurred while processing this directive]